浅谈线段树Segment_Tree

By xiaruize

引言

OI中,有一种好玩的游戏,叫做码线段树,那么线段树是什么???

线段树的目的

线段树主要用于在区间上动态维护一些值(如最大值,最小值,和,积等)

线段树的实现

以区间最大值为例,给定一个长度为 nn 的数组,每次查询求 [l,r][l,r] 之间的最大值,或将 [l,r][l,r] 赋值为 valval

显然,如果暴力去维护这个问题,需要 O(NQ)O(NQ) 的时间复杂度, 并不能解决1≤n,q≤1051 \leq n,q \leq 10^5级别的问题

此时,我们考虑将原问题分解为 ([l,mid][l,mid] 的 maxmax 与 [mid+1,r][mid+1,r] 的 maxmax) 的 maxmax

接着,我们可以以此类推,细分到只有一个节点

当 n=6n=6 时, 线段树如下图

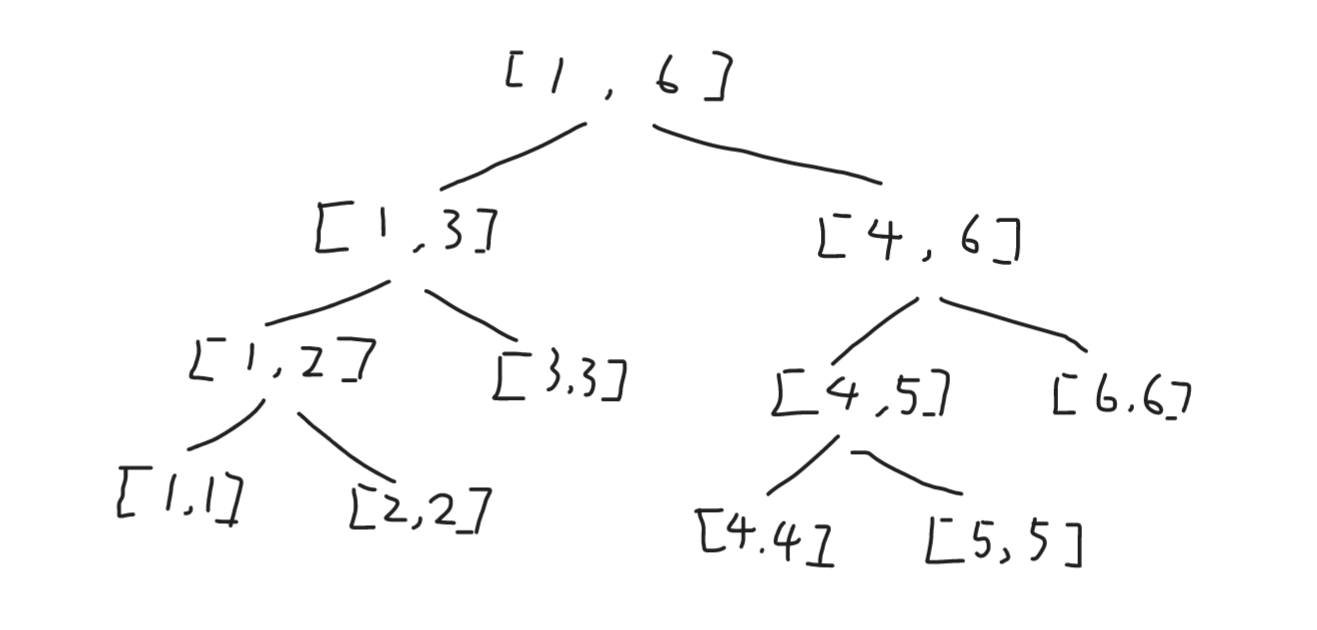
线段树的存储

一般线段树使用和二叉树类似的方式存储注意4倍空间\color{red}{注意4倍空间}

这样存储的好处在于,对于点pp, 它的左儿子是$ p<<1 $, 右儿子是 p<<1∣1p<<1|1, 父节点是 p>>1p>>1

建议使用define定义ls,rs为左右儿子

上传pushup

该操作用于通过pp节点的儿子更新pp节点

以求最大值为例

1
2
3
4
void pushup(int p)
{
    seg[p].val=max(seg[ls].val,seg[rs].val);
}

建树 build

首先,肯定需要建树,递归即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void build(int l,int r,int p)
{
    seg[p].l=l;
    seg[p].r=r; //可以放在函数的参数里
    if(l==r) //到叶子节点
    {
        seg[p].val=a[l]; //赋值
        return;
    }
    int mid=(l+r)>>1; //不打括号也可以,+的优先级比>>高
    build(l,mid,ls); //处理左儿子
    build(mid+1,r,rs); //处理右儿子
    pushup(p); //更新当前节点
}

也可以将当前的区间放在参数里,主要看个人习惯

修改update

单点修改

如果只需要修改一个点,那么可以通过 l,rl,r 的指引, dfsdfs 到这个点,修改它的值,返回时进行一遍 pushuppushup

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void update(int p,int d,int val)
{
    if(seg[p].l==seg[p].r) //到达需要修改的节点
    {
        seg[p].val=d;
        return;
    }
    int mid=seg[p].l+seg[p].r>>1;
    if(d<=mid)//在左侧
        update(ls,d,val);
    if(d>mid)//在右侧
        update(rs,d,val);
    pushup(p); //更新当前节点
}

区间修改(lazy tag)

我们在回头看一下题目,发现需要支持区间修改,如果做nn次单点修改,会消耗大量的时间

此时,我们可以在一段在子节点都需要修改的节点上打一个懒标记(lazy tag),表示当前节点及下属的节点都需要修改

例如,修改区间[1,5]为2

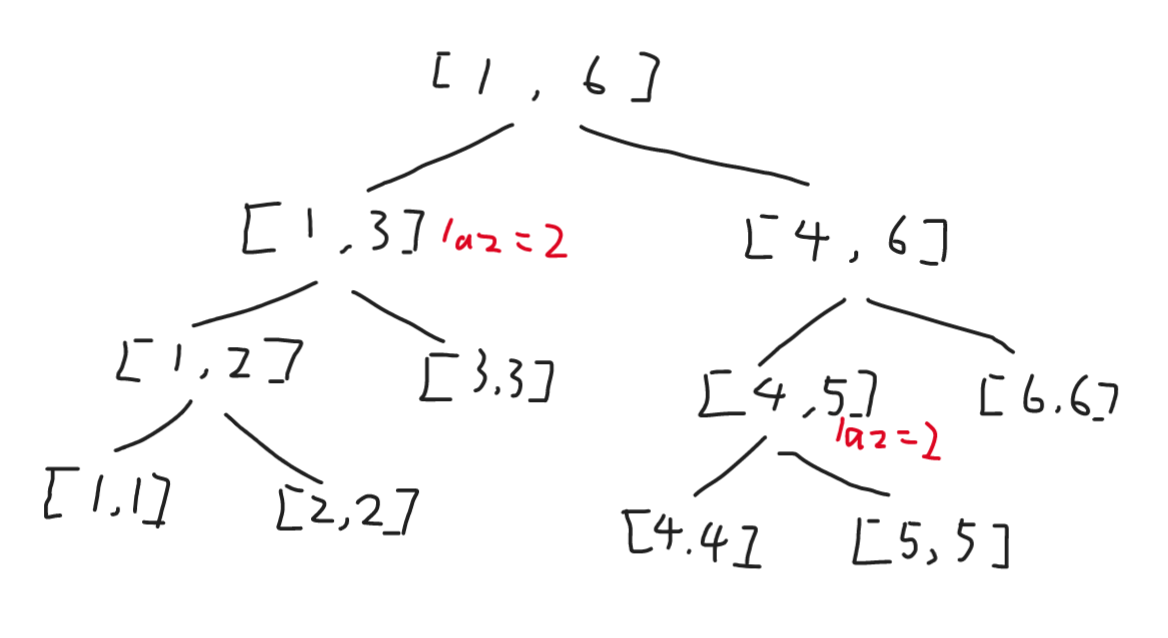
这样,可以用更优的速度完成修改操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void update(int u, int l, int r, int d)
{
    if (tr[p].l >= l && tr[p].r <= r)  //更新节点并打懒标记
    {
        tr[p].val=max(tr[u].val,d);
        tr[p].laz=max(tr[u].laz,d);
    }
    else
    {
        pushdown(p); //见下方
        int mid = tr[p].l + tr[p].r >> 1;
        if (l <= mid) update(ls, l, r, d); //左侧存在需要修改的节点
        if (r > mid) update(rs, l, r, d); //右侧存在需要修改的节点
        pushup(p); //更新当前节点
    }
}

下传懒标记pushdown

如果你认真阅读了上面的代码,会发现pushdown函数并没有讲过

那么pushdown的作用其实是下传懒标记

及将父亲节点记录的修改(laz)传给儿子

1
2
3
4
5
6
7
8
void pushdown(int p)
{
    seg[ls].laz=seg[p].laz;
    seg[ls].val=seg[p].laz;
    seg[rs].laz=seg[p].laz;
    seg[rs].val=seg[p].laz;
    seg[p].laz=0;
}

查询 query

那么,已经有了一棵线段树,要如何查询区间最值呢?

可以去模仿update操作,每次询问左区间和右区间,在合并答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int query(int l,int r,int ll,int rr,int p) //把当前区间放在了参数里的写法
{
    if(l>=ll&&r<=rr)
    {
        return seg[p].val; //到达节点,返回答案
    }
    int mid=(l+r)>>1;
    int res=0;
    pushdown(p);//下传懒标记
    if(mid<rr)
        res=max(res,query(mid+1,r,ll,rr,rs)); //通过左区间更新
    if(mid>=ll)
        res=max(res,query(l,mid,ll,rr,ls)); //通过右区间更新
    return res;
}

读到这里,你应该已经可以基本掌握如何码线段树. 但是,要在码线段树的游戏中超过你的同伴,你需要多加练习