图论

图论 (Graph theory) 是数学的一个分支，图是图论的主要研究对象。图 (Graph) 是由若干给定的顶点及连接两顶点的边所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物，连接两顶点的边则用于表示两个事物间具有这种关系。

什么是图？

无向图

像这样的是一个无向图

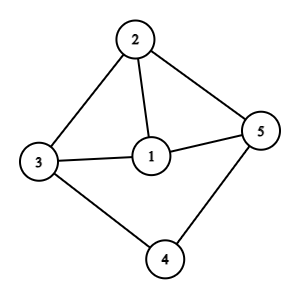
有向图

像这样的是一个有向图

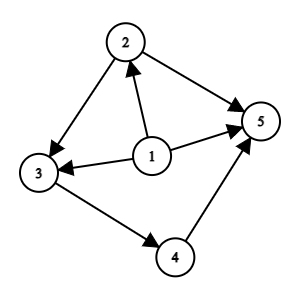
带权图

像这样的是一个带权图

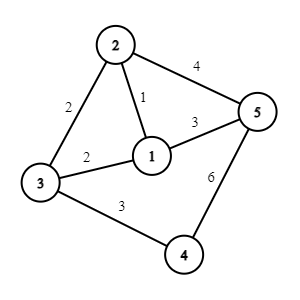
其他基础知识

度数

有几条边连接当前节点

特别对于有向图

入度

指向当前节点的边的数量

出度

从当前节点指向别的节点的边的数量

简单图

简单图指没有“自环和重边”的图

自环

有一个或多个节点有边指向自身的图被称为有自环

重边

两点之间出现两条边(有向图要求是同向的)

存图

常见的存图方式以下几种：

直接存边

很暴力低效，说白了就是把读入数据原封不动的存下来

但是在像Kruskal这种算法中也有应用

邻接矩阵

二维数组Gi,j=0G_{i,j}=0表示没有边,否则Gi,jG_{i,j}存边权或0,10,1表示有没有边

邻接表

邻接表，通过一个vector存图

个人喜好，C++11以后遍历图更好写了

链式前向星

发明者不明，最近几年兴起的

1
2
3
4
5
6
7
8
9
10
11
// head[u] 和 cnt 的初始值都为 -1
void add(int u, int v) {
  nxt[++cnt] = head[u];  // 当前边的后继
  head[u] = cnt;         // 起点 u 的第一条边
  to[cnt] = v;           // 当前边的终点
}

// 遍历 u 的出边
for (int i = head[u]; ~i; i = nxt[i]) {  // ~i 表示 i != -1
  int v = to[i];
}
传说是中国选手整的，支持国货(bushi

最短路

Floyd

优点：

  • 易于实现（我会告诉你就是3个for吗

缺点：

  • 时间复杂度高TLE

disk,x,ydis_{k,x,y}表示只用边1…k, x,y之间的最短距离

可以这样转移disk,x,y=min⁡(disk−1,x,y,disk−1,x,k+disk−1,k,y)dis_{k,x,y}=\min(dis_{k-1,x,y},dis_{k-1,x,k}+dis_{k-1,k,y})

时间复杂度O(n3)O(n^3)

1
2
3
4
5
6
7
for (k = 1; k <= n; k++) {
  for (x = 1; x <= n; x++) {
    for (y = 1; y <= n; y++) {
      f[k][x][y] = min(f[k - 1][x][y], f[k - 1][x][k] + f[k - 1][k][y]);
    }
  }
}

Dijkstra

最实用的最短路算法，好写，复杂度低

维护dis数组表示从s到每个点的距离

初始状态为diss=0dis_s=0，其它为INFINF

每次在所有确定距离且没有被用作为中间节点的点中选择距离最短的，尝试优化周围点的距离

暴力复杂的为O(n2+m)O(n^2+m)

可以使用priority_queue进行优化，把查询最小值的复杂度降到loglog级别，O((n+m)logn)O((n+m)logn)

邻接表存图:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
vector<pair<int,int>> g[N];
int n,m;
int s;
int dis[N];
bool vis[N];

void dijkstra()
{
	priority_queue<pii,vector<pii>,greater<pii>> q;
	memset(dis,0x3f,sizeof(dis));
	dis[s]=0;
	q.push(mk(0,s));
	while(!q.empty())
	{
		int v=q.top().sec;
		q.pop();
		if(vis[v])
			continue;
		vis[v]=true;
		for(auto x:g[v])
		{
			if(dis[v]+x.sec<dis[x.fir]&&!vis[x.fir])
			{
				dis[x.fir]=dis[v]+x.sec;
				q.push(mk(dis[x.fir],x.fir));
			}
		}
	}
}