网络流 - 最大流

概念

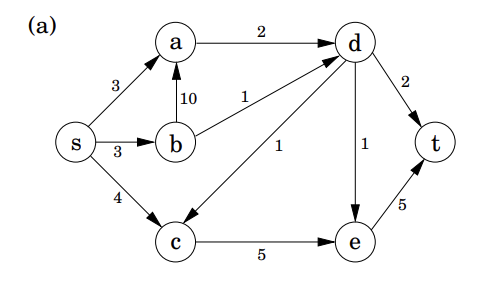
Figure7.4_a_.png

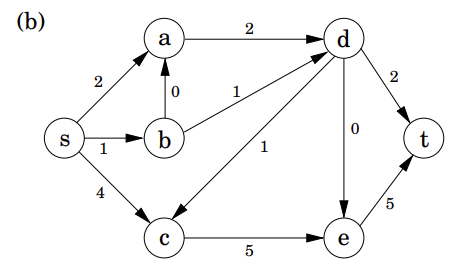
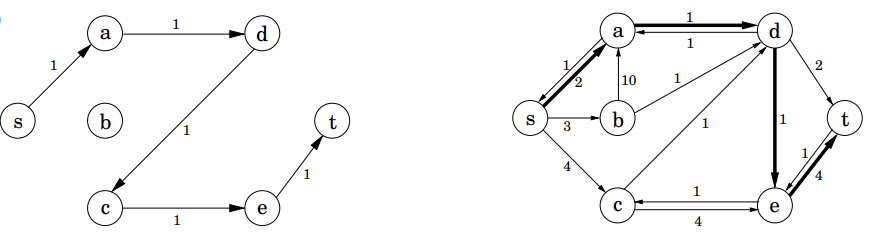
如上图(a)中，

  • ss 为源点
  • tt 为汇点
  • s→as \rightarrow a 上的 33 为这条边的流量
  • 最大流为：假设从源点有足够的流量进入网络，最后能汇到汇点的最大流量

Ford-Fulkerson

Figure7.4_a_.png

再次观察这个图，容易想到一个感性的做法，即从 ss 开始 dfs，直到不能继续增加流量为止

image.png

如上图为一种可行的方式

但是，反复尝试发现，这个方式并不一定能找到最优解，因为每次 dfs 得到的路径并不一定为最优路径

因此，需要在算法中支持撤销操作

使用反向边来达成这一目标，即每次通过后建一条流量等于通过流量的反向边

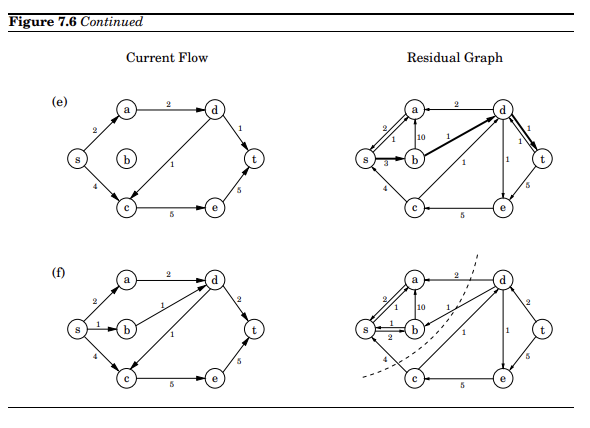
image.png

如图，即为选定 s→a→d→c→e→ts \rightarrow a \rightarrow d \rightarrow c \rightarrow e \rightarrow t 这条路径后的残量网络(显然，流量=最小边权)

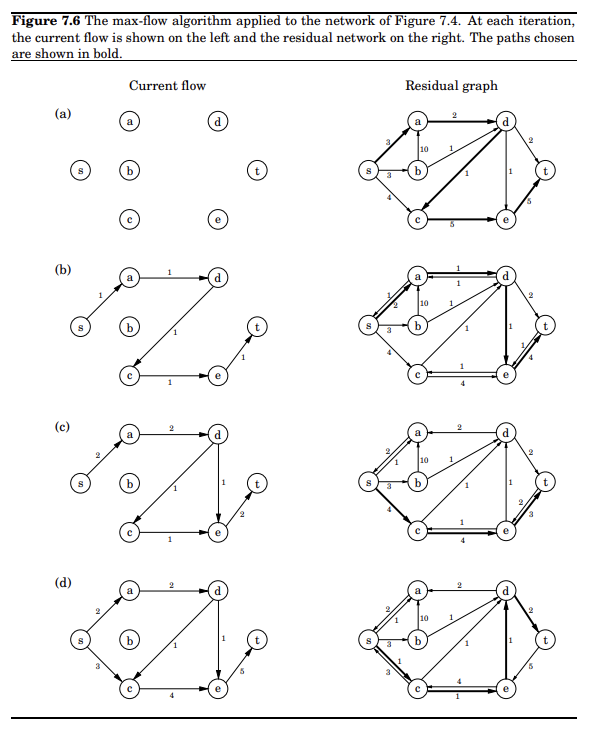
image.png

image.png

上图为该算法的完整流程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int n, m, s, t; // s是源点，t是汇点
bool vis[MAXN];
int dfs(int p = s, int flow = INF)
{
    if (p == t)
        return flow; // 到达终点，返回这条增广路的流量
    vis[p] = true;
    for (int eg = head[p]; eg; eg = edges[eg].next)
    {
        int to = edges[eg].to, vol = edges[eg].w, c;
        // 返回的条件是残余容量大于0、未访问过该点且接下来可以达到终点（递归地实现）
        // 传递下去的流量是边的容量与当前流量中的较小值
        if (vol > 0 && !vis[to] && (c = dfs(to, min(vol, flow))) != -1)
        {
            edges[eg].w -= c;
            edges[eg ^ 1].w += c;//取反向边
            // 建图时要把cnt置为1，且要保证反向边紧接着正向边建立
            return c;
        }
    }
    return -1; // 无法到达终点
}
int FF()
{
    int ans = 0, c;
    while ((c = dfs()) != -1)//寻找路径
    {
        memset(vis, 0, sizeof(vis));
        ans += c;//增加答案
    }
    return ans;
}

时间复杂度：玄学，上限很高

Edmond-Karp

graph 10.png

注意到，在这个图中运行上述代码时，可能会占用较高的时间，因为 a→ba \rightarrow b 会被反复经过

优化：每次选择最短的路径(即使用bfs实现Ford-Fulkerson算法)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
int n, m, s, t, last[MAXN], flow[MAXN];
inline int bfs()
{
    memset(last, -1, sizeof(last));
    queue<int> q;
    q.push(s);
    flow[s] = INF;
    while (!q.empty())
    {
        int p = q.front();
        q.pop();
        if (p == t) // 到达汇点，结束搜索
            break;
        for (int eg = head[p]; eg; eg = edges[eg].next)
        {
            int to = edges[eg].to, vol = edges[eg].w;
            if (vol > 0 && last[to] == -1) // 如果残余容量大于0且未访问过（所以last保持在-1）
            {
                last[to] = eg;
                flow[to] = min(flow[p], vol);
                q.push(to);
            }
        }
    }
    return last[t] != -1;
}
inline int EK()
{
    int maxflow = 0;
    while (bfs())
    {
        maxflow += flow[t];
        for (int i = t; i != s; i = edges[last[i] ^ 1].to) // 从汇点原路返回更新残余容量
        {
            edges[last[i]].w -= flow[t];
            edges[last[i] ^ 1].w += flow[t];
        }
    }
    return maxflow;
}

这就是 Edmond-Karp 算法
时间复杂度：上限 O(ve2)O(ve^2) ， 实际上在大多数情况下跑不满

Dinic

在 OI 中， Dinic 算法因为较为优秀的时间复杂度和较简单的代码实现，最常被使用

  • 先以每个点到 ss 的距离对点分层，暂时删除所有由更深层指向浅层的边(代码实现中不一定要真正删除)

  • dfs 求出当前分层图的最大流

  • 与原图合并

  • 重复上述过程，直到不存在 s→vs\rightarrow v 的路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
struct MF
{
    struct edge
    {
        int v, nxt, cap, flow;
    } e[N];

    int fir[N], cnt;

    int n, S, T;
    int maxflow;
    int dep[N], cur[N];

    void init()
    {
        memset(fir, -1, sizeof fir);
        cnt = 0;
        maxflow = 0;
    }

    void addedge(int u, int v, int w)
    {
        e[cnt].v = v;
        e[cnt].nxt = fir[u];
        e[cnt].cap = w;
        e[cnt].flow = 0;
        fir[u] = cnt++;
        e[cnt].v = u;
        e[cnt].nxt = fir[v];
        e[cnt].cap = 0;
        e[cnt].flow = 0;
        fir[v] = cnt++;
    }

    bool bfs()//分层
    {
        queue<int> q;
        memset(dep, 0, sizeof(int) * (n + 1));

        dep[S] = 1;
        q.push(S);
        while (q.size())
        {
            int u = q.front();
            q.pop();
            for (int i = fir[u]; ~i; i = e[i].nxt)
            {
                int v = e[i].v;
                if ((!dep[v]) && (e[i].cap > e[i].flow))
                {
                    dep[v] = dep[u] + 1;
                    q.push(v);
                }
            }
        }
        return dep[T];
    }

    int dfs(int u, int flow)
    {
        if ((u == T) || (!flow))//找到流
            return flow;

        int ret = 0;
        for (int &i = cur[u]; ~i; i = e[i].nxt)
        {
            int v = e[i].v, d;
            if ((dep[v] == dep[u] + 1) &&//不向浅层转移
                (d = dfs(v, min(flow - ret, e[i].cap - e[i].flow))))//还存在路径
            {
                ret += d;
                e[i].flow += d;
                e[i ^ 1].flow -= d;
                if (ret == flow)
                    return ret;
            }
        }
        return ret;
    }

    void dinic()
    {
        while (bfs())
        {
            memcpy(cur, fir, sizeof(int) * (n + 1));
            maxflow += dfs(S, INF);
        }
    }
} mf;

时间复杂度：上限 O(v2e)O(v^2e) ，实际跑不满

例题

引用